จึงจะหยิบยกเอาส่วนที่คำนวนเกี่ยวกับพลังงานของ scattered particles มาพิจารณากัน เนื่องจากว่าห่างหายไปพอควรกับ blog นี้ก็เลยถือโอกาศมาขยับกันหน่อย ในเรื่องนี้ผมยังทำ GUI เหมือนเดิมอย่าพึ่งตกใจว่าพูดถึงฟิสิกส์มากไป มีความจำเป็นที่ต้องกล่าวถึงที่มาที่ไปจริงๆครับ วางแผนไว้ว่าจะแบ่งเป็นสี่ตอนครับ ทฤษฎีสองตอน ทำ GUI สองตอนครับ (หวังไว้ว่าอย่างนั้น) กลับมาที่ Rutherford scattering กันต่อ เราจะเริ่มด้วยการพิจารณา
$\textbf{Kinematics of Elastic Collisions}$
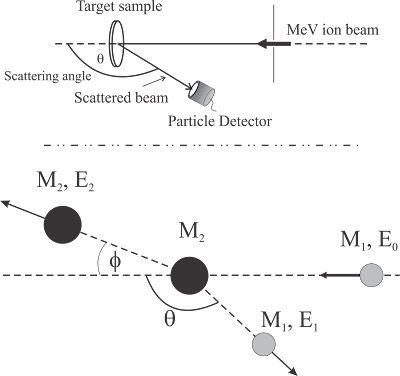
สำหรับ RBS นั้นเราจะเริ่มต้นด้วย การระดมยิ่งด้วย ไอออนที่มีพลังงานค่าเดียว (Monoenergetic particles) ไปยัง อะตอมของธาตุเป้า (Target atoms) เราเรียกไอออนที่เข้าไปชนว่า Incident ions หรือ Projectile ions ภาษาไทยขอเรียกว่า ไอออนกระสุน ตามเอกสารอ้างอิง [1] หลังจากชนแล้วไอออนกระสุนบางตัวจะกระเจิงกลับหลัง (Back scattering) มาตกกระทบที่หัววัด ทำให้ทราบว่าไอออนตัวนั้นกระเจิงออกมาแล้วเหลือพลังงานเท่าไร หลักการของหัววัดจะกล่าวถัดไป รูปด้านล่างเป็นการจัดชุดการทดลอง RBS
รูปที่ 1 ลักษณะการจัดวางเครื่องมือสำหรับการทดลอง RBS (บน) และ Elastic collision รูปนี้เขียนมาจาก เอกสารอ้างอิงที่ [2]
จากรูป ไอออนกระสุนมีมวล ความเร็ว และพลังงานเป็น $M_{1},\;v_{0}$ และ $E_{0}$ วิ่งเข้าไปชน อะตอมของธาตุเป้าที่อยู่นิ่ง มีมวลเป็น $M_{2}$ หลังจากชน ไอออนกระสุนกระเจิงกลับหลังด้วยมุม $\theta$ เรียกว่า Scattering angle โดยมีความเร็วและพลังงานเป็น $v_{1}$ และ $E_{1}$ ส่วนอะตอมของธาตุเป้า เคลื่อนที่ถอยหลังไปด้วยมุม $\phi$ มีความเร็วและพลังงานเป็น $v_{2}$ และ $E_{2}$ เรียก ว่า Recoil atom
การพิจารณาการถ่ายโอนพลังงานของการชนแบบไม่ยืดหยุ่น จะอาศัยกฎการอนุรักษ์พลังงาน และกฎการอนุรักษ์โมเมนตัม ซึ่งสามารถเขียนออกมาเป็นสมการดังนี้
$ (1)\;\;\;\;\;\;\;\;\;\; \frac{1}{2}M_{1}v_{0}^{2}=\frac{1}{2}M_{1}v_{1}^{2}+\frac{1}{2}M_{2}v_{2}^{2} $
$ (2)\;\;\;\;\;\;\;\;\;\;M_{1}v_{0}=M_{1}v_{1}cos\theta +M_{2}v_{2}cos\phi $
$ (3)\;\;\;\;\;\;\;\;\;\;0=M_{1}v_{1}sin\theta-M_{2}v_{2}sin\phi $
จากนั้นเราจะหาค่าอัตราส่วน $\frac{E_{1}}{E_{0}}$ หรือเรียกว่า $Kinematic\;factor\;\;K=\frac{E_{1}}{E_{0}}$
เริ่มจากกำจัดตัวแปร $\phi$ ทิ้งก่อน โดยการ ยกกำลังสองของสมการ 2 และ 3 แล้วจับมาลบกันจะได้สมการดังนี้
$ (4)\;\;\;\;\;\;\;\;\;\;M_{1}^{2}v_{0}^{2}=M_{2}^{2}v_{2}^{2}-M_{1}^{2}v_{1}^{2}+2M_{1}^{2}v_{0}v_{1}cos\theta$
จัดรูปใหม่ เพื่อกำจัด $v_{2}$ โดยเขียนสมการได้ดังนี้
$ (5)\;\;\;\;\;\;\;\;\;\;M_{2}^{2}v_{2}^{2}=M_{1}^{2}v_{1}^{2}+M_{1}^{2}v_{0}^{2}-2M_{1}^{2}v_{0}v_{1}cos\theta$
จากนั้นนำสมการที่ 5 ไปแทนในสมการที่ 1 จะได้สมการดังนี้
$ (6)\;\;\;\;\;\;\;\;\;\;M_{1}v_{0}^{2}=M_{1}v_{1}^{2}+\frac{M_{1}^{2}}{M_{2}}v_{0}^{2}+\frac{M_{1}^{2}}{M_{2}}v_{1}^{2}-2\frac{M_{1}^{2}}{M_{2}}v_{0}v_{1}cos\theta$
จากนั้น หารตลอดด้วย $M_{1}v_{0}^{2}$ และจัดรูปเป็นสมการกำลังสอง ได้ดังนี้
$ (7)\;\;\;\;\;\;\;\;\;\;0=(1+\frac{M_{1}}{M_{2}})(\frac{v_{1}}{v_{0}})^2-(\frac{2M_{1}cos\theta}{M_{2}})(\frac{v_{1}}{v_{0}})+(\frac{M_{1}}{M_{2}}-1)$
จากนั้นก็แก้สมการกำลังสอง จะได้คำตอบคือ
$ (8)\;\;\;\;\;\;\;\;\;\;\frac{v_{1}}{v_{0}}=\frac{M_{1}cos\theta}{M_{1}+M_{2}}\pm [(\frac{M_{1}}{M_{1}+M_{2}})^2cos^2\theta+(\frac{M_{2}-M_{1}}{M_{1}+M_{2}})]^{1/2}$
หรือ
$ (9)\;\;\;\;\;\;\;\;\;\;\frac{v_{1}}{v_{0}}=\frac{M_{1}cos\theta\pm[M_{2}^{2}-M_{1}^{2}sin^2\theta]^{1/2}}{M_{1}+M_{2}}$
สำหรับอัตราส่วนของพลังงาน เมื่อ $M_{1}<M_{2}$ จะเขียนได้ว่า
$ (10)\;\;\;\;\;\;\;\;\;\;\frac{E_{1}}{E_{0}}=[\frac{M_{1}cos\theta+[M_{2}^{2}-M_{1}^{2}sin^2\theta]^{1/2}}{M_{1}+M_{2}}]^2$
โดยที่ $Kinematic\;factor,\;K=[\frac{M_{1}cos\theta+[M_{2}^{2}-M_{1}^{2}sin^2\theta]^{1/2}}{M_{1}+M_{2}}]^2$
ดังนั้น $E_{1}=KE_{0}$ หากย้อนไปพิจารณาสมการที่ 10 จะเห็นว่าพารามิเตอร์ $E_{0},\;E_{1}$ วัดได้โดยตรงจากหัววัด มุม $\theta$ เซตได้จากการทดลอง $M_{1}$ รู้อยู่แล้วในทางปฏิบัติจาก switching magnet (คัดเลือกมวลและประจุ) หรือใช้แหล่งกำเนิดที่รู้ชนิดของอนุภาคเช่น Alpha source (แต่คงต้องเป็นแหล่งกำเนิดที่แรงหน่อย) ดังนั้นจะเห็นว่าการทดลองนี้สามารถหา องค์ประกอบของตัวอย่างว่าประกอบด้วยธาตุอะไรบ้าง รายละเอียดติดตามได้จากเอกสารอ้างอิง (Refs. 1 และ 2)
ในตอนนี้ต้องจบไว้แค่นี้ครับ แล้วจะมาต่อในตอนถัดไป
References
[1] รองศาสตราจารย์ ดร. สมศร สิงขรัตน์ และ ดร. ธีรศักดิ์ คำวรรณะ, คู่มือแนะนำ เทคนิค RBS, RBS/channeling, PIXE และ IL: 4 เทคนิควิเคราะห์ธาตุด้วยลำไอออนในระดับไมโครเมตรและนาโนเมตร, ศูนย์วิจัยฟิสิกส์ของพลาสมาและลำอนุภาค, ภาควิชาฟิสิกส์และวัสดุศาสตร์ คณะวิทยาศาสตร์ มหาวิทยาลัยเชียงใหม่ 2553
[2] Terry L. Alford, Leonard C. Feldman and James W. Mayer. Fundamentals of Nanoscale Film Analysis, Springer 2007.